Rayleigh Damping Scheme
Rayleigh damping is used in the analysis of soil structures to damp the natural oscillation modes of the system. The dissipation of the ground is modeled through the damping matrix [C], assembling the dissipation matrix of the individual elements (q) using the the following scheme:
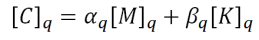
where:
- [M]q = mass matrix of each element
- [C]q = damping matrix of each element
- [K]q = stiffness matrix of each element
- αq = mass-proportional Rayleigh damping constant
- βq = stiffness-proportional Rayleigh damping constant
In a system with a multiple degree-of-freedom, the critical damping ratio, λq at any angular frequency of the system, αq, can be calculated from (Bathe and Wilson 1976):
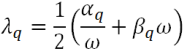
where λq is the fraction on critical damping and ω is the angular frequency.
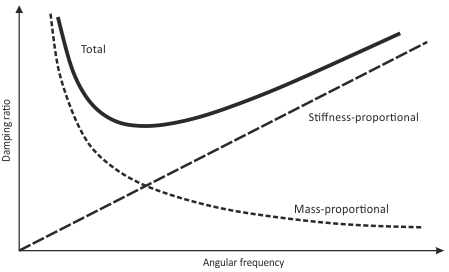The variation of the damping ratio with the angular frequency αq is show in previous picture.
There are three curves: mass-components; stiffness components; and the sum of both components.
The mass-proportional damping is dominant at lower angular-frequency ranges, while stiffness-proportional damping dominates at higher angular frequencies.
The stiffness-proportional damping is linearly proportional to response frequency and the mass proportional damping is inversely proportional to response frequency.
The damping in the ground is independent of the frequency, therefore, the choice of α e β must be made so that the damping values have minimal variations on the frequency range of interest. The constants are choices in such a way the damping is minimized at the fundamental circular frequency of the entire model because the first mode of vibrations has the highest participations factor of all the other modes. For this:
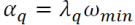
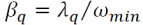
The center frequency of the model is defined as:
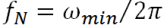
In Quad4M code the coefficients of Rayleigh are calculated as a function of two frequencies α1 e α2 by the following expression for each elements:
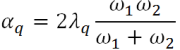
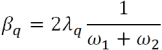
where:
- ω1 = is the minimal angular frequency of the model
- ω2 = n * ω1
- n = closest odd integer that approximates, in exceeding, the ratio of predominant frequency of the seismic input and the natural frequency of the soil structure
For each iteration the average shear strain is computed into each element and the damping curve are consulted for the estimate the correct damping. The value of ω1 (first angular frequency) is computed by solving the following system of equations:
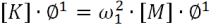
where θ1 is the first mode shape. The fundamental Frequency of the model is calculated at the first iteration.
For example:
- ω1 = the minimal angular frequency = 6.651 [s-1]
- fn = natural frequency = ω1/2π = 1.059 [Hz]
- fi = predominant frequency Horizontal input motion = 3.992 [Hz]
- fi/fn = 3.770 ⇒ closest odd integer greater ⇒ n = 5
- ω2 = n * ω1 = 33.256 [s-1]
The Visual-Q4M automatically calculates the natural frequency of the model.